smpl.functions.lorentz

smpl.functions.lorentz(x, x_0, a, d, y)[source]

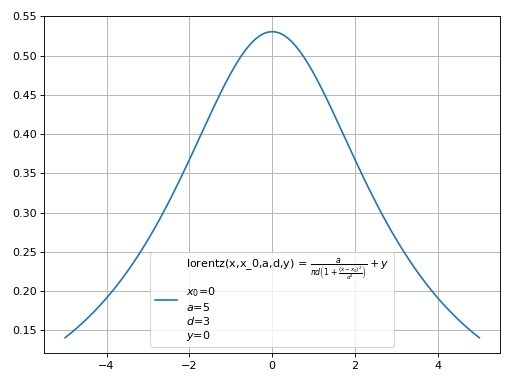
lorentz(x,x_0,a,d,y) = \(\frac{a}{\pi d \left(1 + \frac{\left(x - x_{0}\right)^{2}}{d^{2}}\right)} + y\)

>>> from smpl.functions import lorentz
>>> from smpl import plot
>>> plot.function(lorentz,0,5,3,0,xmin=-5,xmax=5)